絶好調の渡辺明２冠が鬼の棲家で１２戦全勝、斎太郎王座の息の根を止めて昇級の可能性は木村一基九段か行方尚史八段に
既にＡ級復帰を決めている渡辺明にとっては消化試合なのである。相手の斎太郎王座はつ（続きはクリック）
「 2019年03月 」一覧
とりあえず「いだてん」の放映は続くことが判明した慰労会だか決起会だか行われた夜
いつもは送別ランチで使われる会社近くのホテルのレストラン。つい食べ過ぎちゃうし飲（続きはクリック）
【Breaking News】げげげげ！ピエール瀧逮捕、「いだてん」はどうなる！？
これで「いだてん」も不適切動画の仲間入りか（落涙） ↓ にほんブ（続きはクリック）
藤井聡太七段、５１年ぶりの年間勝率記録更新に暗雲が漂う手痛い１敗
藤井聡太が来年度に史上最年少でのタイトル挑戦・獲得を目指す上で、最も早いのが棋聖（続きはクリック）
史上初「M-1」「R-1」２冠の粗品 “高速フリップネタ”は１９歳で完成
ひとつひとつがくだらなくも面白い。それが高速で積み重なってのR-1芸である。個人（続きはクリック）
「Ｒ－１ぐらんぷり ２０１９」現地観覧
やっぱり生（ライブ）はいい。粗品は切れのいいフリップ芸で初のＭ―１・Ｒ―１の２冠（続きはクリック）
泡泡酒座 八之助
今日あったことを全部記すには時間も気力も乏しく、今から寝るしかないので一言だけ「（続きはクリック）
緊急告知とうちのこ
本日は図書館と映画とトークショーと入谷のお店。 そして、明日はＲー１ぐらん（続きはクリック）
台中で一番の猫カフェ「貓‧旅行咖啡輕食館」の投稿、それをのせた理由は
今月２０日からまた台湾へいく。 久しぶりに台中へも行く予定である。（続きはクリック）
私のアルメニア覚え書き (原人舎) 単行本（ソフトカバー） – 2005/8 大場 秀章(著)
外務省の海外渡航情報では大抵レベル1(十分注意してください)以上、ところによって（続きはクリック）
ぺいペイＰａｙぺいペイ五月蝿いな、と思っていたが、Ｊ－Ｃｏｉｎ Ｐａｙの可能性をほんの少し感じた
３月１日からスマートフォン（スマホ）を使ったＱＲコード決済サービスの陣取り合戦に（続きはクリック）
第７７期順位戦Ｃ１級 藤井聡太２期連続&師弟同時昇級を逃すも勝利をもぎとり年度最高勝率更新に大前進
今年度のＣ１級はある意味、Ａ級よりも注目を浴びたかもしれない。杉本昌隆八段＆藤井（続きはクリック）
唐突だが、２０１９年の中日ドラゴンズの予想をしてみる
ぼんくら野球評論家のいい加減な順位予想など当たるはずなどない。同じ当たらない予想（続きはクリック）
第６８回ＮＨＫ杯 将棋準決勝第１局 羽生九段vs丸山九段 ３０分以上放送時間が余る異常事態
これは羽生がすごいのか、丸山がだめなのか。羽生が先手で丸山が後手の一手損角換わり（続きはクリック）
久しぶりの将棋ランキング１位になった日に豊島将之２冠がＡ級順位戦を制し名人挑戦者に
現在のＡ級順位戦で最も勝てる棋士が挑戦者になった、ということでこの結論は当然であ（続きはクリック）
第77期 一番長い日
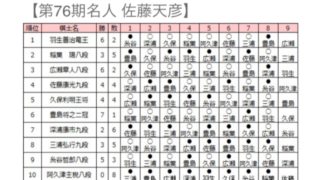
AbemaTV生放送 第77期順位戦A級9回戦 最終一斉対局 名人挑戦者決定！（続きはクリック）
数え年＝元号、であるという新たな知見
数え年の存在や定義は知ってはいたが、この年齢になるまで「何故こんなものが存在する（続きはクリック）